Main Page: Difference between revisions
| (6 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
Treating the blockchain network as an infrastructure for transaction processing, the blockchain protocol solved service reliability problem but not performance challenge. The legacy infrastructure scaling dilemma: performance against reliability remains (where "infrastructure reliability" also does not have a commonly accepted definition). Fortunately these metrics, although important, are non-critical. Solutions that have been proposed have had varying opportunity costs. For many years, there were no obvious solutions that addressed all three blockchain goals (security, decentralization and scalability). | Treating the blockchain network as an infrastructure for transaction processing, the blockchain protocol solved service reliability problem but not performance challenge. The legacy infrastructure scaling dilemma: performance against reliability remains (where "infrastructure reliability" also does not have a commonly accepted definition). Fortunately these metrics, although important, are non-critical. Solutions that have been proposed have had varying opportunity costs. For many years, there were no obvious solutions that addressed all three blockchain goals (security, decentralization and scalability). | ||
== Statistic Multiplexed Computing (SMC) == | == Statistic Multiplexed Computing (SMC) == | ||
The principle of using unreliable components to build an arbitrarily reliable system was first lectured by von Neumann in the early 1950s<ref>https://static.ias.edu/pitp/archive/2012files/Probabilistic_Logics.pdf</ref>. The original idea was to use probabilistic logic to quantify the arbitrary reliability of a system by multiplexing all components. This theory was applied to the construction of Internet protocols to deliver the "best effort" reliability. | The principle of using unreliable components to build an arbitrarily reliable system was first lectured by von Neumann in the early 1950s<ref>https://static.ias.edu/pitp/archive/2012files/Probabilistic_Logics.pdf</ref>. The original idea was to use probabilistic logic to quantify the arbitrary reliability of a system by multiplexing all components. This theory was applied to the construction of Internet protocols to deliver the "best effort" reliability. Ironically, "best effort reliability" also enabled "best effort" performance which in turn enabled "best effort" scalability of the Internet. The same cannot be said to computing infrastructures. | ||
The critical flaw in existing computing infrastructures is the assumed network and processor's reliability. This is exactly what the blockchain protocols have avoided. Therefore, the Bitcoin network demonstrated unprecedented service reliability and tamper resistance. As will be explained in this space, the SMC principles can also resolve blockchain's scalability challenge. This is a natural extension of the Internet protocol revolution for mission critical service infrastructures. Unlike existing blockchain protocols, the SMC powered blockchain protocol is applicable to centralized and decentralized applications. It paves the path for seamless integration of Web2.0 and Web3.0 infrastructures. | |||
SMC technology was developed based on extensive experiences in fault tolerant high performance computing and rigorous impossibility studies. For details, click [[SMC|'''''here''''']]. | |||
== Definitions == | == Definitions == | ||
'''Infrastructure scalability''' does not have a commonly accepted definition. It helps to define the challenging metrics more precisely before the infrastructure protocol design. In the following | '''Infrastructure scalability''' does not have a commonly accepted definition. It helps to define the challenging metrics more precisely before the infrastructure protocol design. In the following, the word "'''infrastructure'''" means any '''application running on the infrastructure.''' | ||
# '''Infrastructure Reliability''': MTBF (mean time between failure) = <math>\frac{\sum ((Start-Of-Downtime) - (Start-of-uptime)) }{No-of-failures}</math> | # '''Infrastructure Reliability''': MTBF (mean time between failure) = <math>\frac{\sum ((Start-Of-Downtime) - (Start-of-uptime)) }{No-of-failures}</math> | ||
| Line 52: | Line 56: | ||
# '''Infrastructure Scalability''': Expanding the infrastructure in number of processors, networks or storage should have '''incrementally better''' impacts on application reliability and performance. | # '''Infrastructure Scalability''': Expanding the infrastructure in number of processors, networks or storage should have '''incrementally better''' impacts on application reliability and performance. | ||
# '''Record Immutability''': For transaction ledgers, all confirmed records and changes are final. This is required by the blockchain protocol. | # '''Record Immutability''': For transaction ledgers, all confirmed records and changes are final. This is required by the blockchain protocol. | ||
Note that in practice, record immutability is much harder to achieve than expected. There are two challenges, a) 51% attacks can literally wipe out all histories if successful, and b) for protocols require all nodes to hold independently verified ledger, such as the Bitcoin, the storage requirement grows approximately 50GB per month. | Note that in practice, record immutability is much harder to achieve than expected. There are two challenges, a) 51% attacks can literally wipe out all histories if successful, and b) for protocols require all nodes to hold independently verified ledger, such as the Bitcoin, the storage requirement grows approximately 50GB per month. It is conceivable that the chain would collapse when all nodes' storage capacity is saturated. Dividing the chain into fixed "shards" can mitigate the eventuality for a while but cannot avoid the ultimate demise. | ||
== Protocol Design and Proofs == | == Protocol Design and Proofs == | ||
| Line 79: | Line 83: | ||
A formal proof requires a parallel computing model, when taking the number of components to infinity, can yield the maximal performance limit under the assumptions. There are two such models: Amdahl's Law <ref>https://en.wikipedia.org/wiki/Amdahl%27s_law</ref> and Gustafson's Law <ref>https://en.wikipedia.org/wiki/Gustafson%27s_law</ref>. | A formal proof requires a parallel computing model, when taking the number of components to infinity, can yield the maximal performance limit under the assumptions. There are two such models: Amdahl's Law <ref>https://en.wikipedia.org/wiki/Amdahl%27s_law</ref> and Gustafson's Law <ref>https://en.wikipedia.org/wiki/Gustafson%27s_law</ref>. | ||
The Amdahl's Law assumes 0<= ''s'' <=1 percentage of serial instructions that cannot be parallelized. Then the ''(1-s)'' percentage of instructions can be accelerated using ''p'' processors. | The Amdahl's Law assumes (0<= ''s'' <=1), a percentage of serial instructions that cannot be parallelized. Then the ''(1-s)'' percentage of instructions can be accelerated using ''p'' processors. The Speedup can then be expressed as: | ||
<div style="text-align: center;"> | <div style="text-align: center;"> | ||
Speedup(p) = <math>{1 \over s + {(1-s) \over p}}</math> (1) <br>Speedup(<math>\lim_{p \to \infty}</math>) = <math>\frac{1}{s}</math> (2) | Speedup(p) = <math>{1 \over s + {(1-s) \over p}}</math> (1) <br>Speedup(<math>\lim_{p \to \infty}</math>) = <math>\frac{1}{s}</math> (2) | ||
</div> | </div> | ||
Taking ''p'' to infinity in equation (1) yields equation (2). But this "scaling" step has two different operational semantics: a) increasing ''p'' for faster acceleration by reducing the value of (''1-s)/p'' solving the same problem. This will result ''s'' asymptotically approaching 1. Thus the speedup is above bounded to 1. Or b) increasing ''p'' to increase the parallel instruction percentage ''(1-s)'' by solving bigger problems. This will force ''s'' asymptotically approach 0. Then the speedup is | Taking ''p'' to infinity in equation (1) yields equation (2). But this "scaling" step has two different operational semantics: a) increasing ''p'' for faster acceleration by reducing the value of (''1-s)/p'' solving the same problem. This will result ''s'' asymptotically approaching to 1. Thus the speedup is above bounded to 1. Or b) increasing ''p'' to increase the parallel instruction percentage ''(1-s)'' by solving bigger problems. This will force ''s'' asymptotically approach to 0. Then the speedup is unbounded <math>\infty</math>. This scaling ambiguity has caused more than half century of confusion in the community. | ||
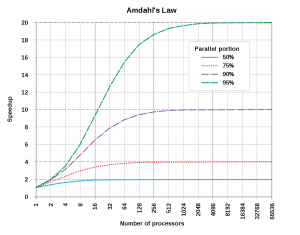
Although quantifying ''s'' requires defining the problem size, | Although quantifying ''s'' requires defining the problem size, equations (1) and (2) are equally applicable to any programs solving any problem size with any percentage ''s''. The limit of speedup (2) also does not depend on problem size. However, since Amdahl originally used fixed problem sizes to argue for the validity of not building parallel machines with too many processors, assuming fixed problem size using ''p'' processors has been the norm in interpreting Amdahl's law in the past. This assumption has led to the dismal speedup predictions.[[File:Amdahl's Law.png|thumb|Amdahl's Law Speedup Predictions|center]]This Amdahl's Law interpretation seems to suggest parallel performances following the economic law of diminishing of returns, even though the mathematics model implies more potentials. | ||
In 1988, Gustafson and Barsis at the Sandia National Laboratory conducted parallel computing experiments that seem to suggest potential infinite speedup. | In 1988, Gustafson and Barsis at the Sandia National Laboratory conducted parallel computing experiments that seem to suggest potential infinite speedup. | ||
Gustafson's Law was based on measured sequential and parallel elapsed times using ''p'' (=1024) processors. A new sequential percentage ''0<=x'<=1'' can be calculated using ''p'' processors. ''(1-x')'' is the parallel percentage using ''p'' processors. | Gustafson's Law was based on measured sequential and parallel elapsed times using ''p'' (=1024) processors. A new sequential percentage (''0<=x'<=1)'' can be calculated using ''p'' processors. ''(1-x')'' is the parallel percentage using ''p'' processors. | ||
To estimate accomplished speedup, Gustafson's Law states: | To estimate accomplished speedup, Gustafson's Law states: | ||
| Line 98: | Line 102: | ||
</div> | </div> | ||
Scaling ''p'' to <math>\infty</math> for equation (3) cannot be done mathematically since ''s''' is dependent on the values of ''p''. | Scaling ''p'' to <math>\infty</math> for equation (3) cannot be done mathematically since ''s''' is dependent on the values of ''p''. For practical applications, the scaling action also has two operational semantics: a) Keep the problem size fixed, adding processors to further reduce the total parallel processing time, this will push for bigger s' asymptotically to 1. Thus speedup is also bounded to 1. Or b) expanding the problem size to allow the parallel part expanded solving bigger problems by simply multiplying (1-''s')'' by ''p (as shown in the chart below)''. Even though the chart is mathematically incorrect, equation (3) can be translated to find the real serial percentage ''s'' under a single processor. Increasing ''p in equation(3)'' will force the translated s asymptotically approaching to 0. Speedup will be above bounded to ''<math>\infty</math> by Amdahl's equation (2)''. | ||
For some reason, in late 1980's, Gustafson's Law was used to argue for Massively Parallel Computing (MPC) (or ManyCPU) experiments and Amdahl's Law was used to argue for bigger mainframe (or BigCPU) computer architectures. These laws have been used to support two diverging computing system experiments and constructions until recent convergence. | |||
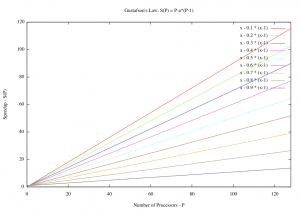
[[File:Gustafson.png|thumb|Gustafson's Law|center]] | [[File:Gustafson.png|thumb|Gustafson's Law|center]] | ||
It | It should now be obvious that the two law are identical with Amdahl's Law more succinct. But Gustafson's formula helps to quantify the serial percentages from practical program instrumentation. In fact, the two serial percentages can be related by a simple equation<ref>https://www.researchgate.net/publication/228367369_Reevaluating_Amdahl's_law_and_Gustafson's_law</ref>: | ||
<div style="text-align: center;"> | <div style="text-align: center;"> | ||
| Line 106: | Line 112: | ||
</div> | </div> | ||
Both laws actually refer to the same mathematical abstraction. Gustafson's formula assists in quantifying the percentage of serial computing through | Both laws actually refer to the same mathematical abstraction. Gustafson's formula assists in quantifying the percentage of serial computing through parallel instrumentation. Amdahl's Law then delivers the ultimate predictions. This should have cleared the half-century myth about scaled-speedup and unscaled-speedup. | ||
In practice, extracting parallelism from an algorithm to use more processors is much harder than simply expanding the already parallelized parts to solve bigger problems. This explanation can be validated in practice when developers routinely increasing the problem size to use more parallel processors. | In practice, extracting parallelism from an algorithm to use more processors is much harder than simply expanding the already parallelized parts to solve bigger problems. This explanation can be validated in practice when developers routinely increasing the problem size to use more parallel processors. | ||
| Line 116: | Line 122: | ||
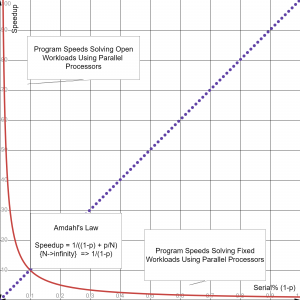
[[File:DiminishingReturn2.png|alt=infinite Speedup Under Amdahl's Law|center|thumb|Infinite Speedup in Amdahl's Law|400x400px]] | [[File:DiminishingReturn2.png|alt=infinite Speedup Under Amdahl's Law|center|thumb|Infinite Speedup in Amdahl's Law|400x400px]] | ||
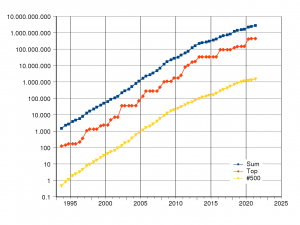
The TOP500 supercomputer competition provides another proof by a historical log of unrelenting computation power growths where the | The TOP500 supercomputer competition provides another proof by a historical log of unrelenting computation power growths where the benchmark (Linpack) having no problem size limit. All manufacturers compete for the world's fastest supercomputer race <ref>https://www.top500.org/</ref> solving the largest possible Linpack problem that can be handled by the hardware. The follow chart illustrates the continuous speed improvements by year. | ||
[[File:Supercomputers-history.png|center|thumb]] | [[File:Supercomputers-history.png|center|thumb]] | ||
In practical blockchain applications, the number of transactions to be processed will increase without a | In practical blockchain applications, the number of transactions to be processed will increase without a bound. The ledger storage will continue to grow. In practice, the available computing, networking and storage components will continue to grow without bound enabled by the networking protocols. Therefore it is possible to build an infinitely scalable blockchain with these assumption. In particular, a statistic multiplexed computing blockchain can meet any future application needs given proper economic incentives. The infrastructure no longer has the structural deficiency. | ||
== Action Plan == | == Action Plan == | ||
Latest revision as of 09:20, 16 October 2024
Welcome to Toi-Twiki -- A Toichain Wiki
This is the unofficial Toichain wiki site. Content is subject to changes.
Introduction
The blockchain protocol was introduced in a seminal paper entitled "Bitcoin: A peer-to-peer Electronic Cash System" [1] by Satoshi Nakamoto in 2008. Although there were previous peer-to-peer file-sharing projects such as Napster [2], BitTorrent [3] and other electronic currency/file sharing applications, Bitcoin is the most enduring among the 23,000+ blockchains. Unlike other cryptocurrencies, the Bitcoin is often referred to as "digital gold" since the total coin supply is limited to 21 million (hard-coded in all running programs) and the only way to earn coin is to participate in the transaction block validation process. Token(or coin) supply and their disbursement policies differ among protocols.
The most attractive common blockchain features are 1) a decentralized consensus-driven decision making process and 2) a step-by-step cryptographic proving system. While blockchain is best known as a cryptocurrency transaction processing and record-keeping system, there are many other applications that can benefit from the secure storage, reliable transaction ledgers, fault tolerance and tamper resistance features.
Algorithm vs. Protocol
Before trying to understand the Blockchain protocol and its variants, it is important to understand the differences between an algorithm and a protocol.
In general, an algorithm is a program that runs on a single computer solving a single problem. A protocol, however, is a program that runs on all computers in parallel solving a single problem. An algorithm must be transformed to run on all computers in parallel solving the same problem before it to be called a protocol. Therefore, protocol development is significantly more difficult than algorithms.
Consensus Protocols
A good consensus protocol in a blockchain system has at least four properties:
- Fault tolerance to defend failures caused by natural disasters and human hacks or accidents
- Byzantine failure tolerance to defend exploitation by colluding parties
- Centralization avoidance to prevent corruptions in the decision making process
- Source code tamper resistance to automatically reject malicious attacks
Without assuming all nodes are active at all times, the blockchain relies on "gossip" protocol to communicate with other nodes. There are two popular types of consensus protocols: Proof of Work (PoW) [4] or Proof of Stake (PoS) [5]. Others include Proof of Possession(PoP)[6] and Proof of History(PoH)[7]. The ultimate goal is to eliminate double-spending. Since most projects are open source, it's easy for a malicious actor to tamper a few nodes. This shouldn't compromise network integrity.
The Bitcoin network uses PoW which forces participating miners to compete for the fastest hashing rate by solving a computational cryptographic puzzle. Although it withstood more than 14 years of use, Bitcoin has been criticized for escalating electricity consumption [8]. Other blockchain designs have experienced different challenges. For example, the PoH network Solana suffered multiple single-point-failure incidents [9]. All protocols struggle to combat scaling challenges. All are susceptible to 51% attacks [10].
Since 2009, Bitcoin has proven to be the strongest and least susceptible to common hacks [11]. As the PoW puzzle difficulty has increased dramatically over the years, the probability of a 51% attack on the Bitcoin network becomes more difficult. PoS protocols can save more than 90% energy consumption compared to PoW chains. But PoS chains have higher risks than PoW chains since a stolen coin will grow in PoS chains (for increased probability to be selected) forever but not in PoW chains (only hash rates count). PoS community governance rules can mitigate the voting power centralization problem. Staking and slashing policies can incentivize good behaviors and punish bad ones. In either case, double-spend is very expensive and difficult. According to Forbes, there are 80 cryptocurrencies that use PoS protocols at the time of this writing.
There are approximately 1,000 blockchains in four types: public, private, consortium, and permissioned [12].
Cryptographic Proofs
Bitcoin protocol relies on UTXO (unspent transaction output) model and lock-step cryptographic proofs to authenticate every transaction. Once spent, the UTXO is destroyed. Double-spending is theoretically impossible. Each proof step must be executed on a script engine running the same protocol on all nodes. The concurrently produced results are confirmed by the consensus protocol mentioned above and committed to the chain.
Centralized vs. Decentralized Applications
The Bitcoin protocol enabled decentralized processing of traditionally centrally processed transactions without any trusted third-party. It inspired many decentralized financial applications, especially for applications with very long payment chains. However for fraud prevention and meeting financial regulatory requirements, many practical applications still require KYC (know your customer) checks. It is not possible to eliminate all trusted third parties, especially for custodial financial applications. There is a clear need for decentralized processing of trusted authority applications.
Blockchain Trilemma
Blockchain protocols have three common aspects (goals): security, decentralization and scalability -- these three terms do not have precise definitions but are intuitively understood [13]. To date, existing cryptographic tools have been proven effective for transaction security before the introduction of smart contracts. Decentralization is given by the nature of the protocols. In theory, there should be no service downtimes unless the entire network is down and all nodes crash at the same time.
A major shortcoming is scalability. Since all nodes verify each transaction independently, they need to store all the information required for it. As the chain grows, this burdens all nodes in the network. There are workarounds by limiting the amount of data stored on some nodes and exploiting the network to retrieve required information, such as the Limited/Light Nodes in Bitcoin network. Vast majority nodes are still full nodes in the existing Bitcoin network. Transaction processing speed often expressed as transactions per second(TPS) of blockchain have to exceed TPS ratings of credit card payment systems like VISA or MasterCard to reap the full benefits of blockchain. This is a tough problem and increasing the block size and/or reducing the block time or difficulty isn't a solution[14]. Since blockchain TPS is very low, the transaction fees is often very high. This discourages public adoption. Layer 2 solution like Lightning Network or ZK-rollups, where only final settlement is on the main chain tend to address these issues. However, one could always argue that this often compromises some aspects of security and/or decentralization to achieve high TPS.
The trilemma was first introduced by Vitalik Buterin[15], one of the co-founders of Ethereum network. The problems he identified are real. There seem to be no obvious solutions that can accomplish all three goals at the same time. Therefore, all proposed solutions revolve around reducing "opportunity costs" focusing only on satisfying partial goals.
Treating the blockchain network as an infrastructure for transaction processing, the blockchain protocol solved service reliability problem but not performance challenge. The legacy infrastructure scaling dilemma: performance against reliability remains (where "infrastructure reliability" also does not have a commonly accepted definition). Fortunately these metrics, although important, are non-critical. Solutions that have been proposed have had varying opportunity costs. For many years, there were no obvious solutions that addressed all three blockchain goals (security, decentralization and scalability).
Statistic Multiplexed Computing (SMC)
The principle of using unreliable components to build an arbitrarily reliable system was first lectured by von Neumann in the early 1950s[16]. The original idea was to use probabilistic logic to quantify the arbitrary reliability of a system by multiplexing all components. This theory was applied to the construction of Internet protocols to deliver the "best effort" reliability. Ironically, "best effort reliability" also enabled "best effort" performance which in turn enabled "best effort" scalability of the Internet. The same cannot be said to computing infrastructures.
The critical flaw in existing computing infrastructures is the assumed network and processor's reliability. This is exactly what the blockchain protocols have avoided. Therefore, the Bitcoin network demonstrated unprecedented service reliability and tamper resistance. As will be explained in this space, the SMC principles can also resolve blockchain's scalability challenge. This is a natural extension of the Internet protocol revolution for mission critical service infrastructures. Unlike existing blockchain protocols, the SMC powered blockchain protocol is applicable to centralized and decentralized applications. It paves the path for seamless integration of Web2.0 and Web3.0 infrastructures.
SMC technology was developed based on extensive experiences in fault tolerant high performance computing and rigorous impossibility studies. For details, click here.
Definitions
Infrastructure scalability does not have a commonly accepted definition. It helps to define the challenging metrics more precisely before the infrastructure protocol design. In the following, the word "infrastructure" means any application running on the infrastructure.
- Infrastructure Reliability: MTBF (mean time between failure) =
- Infrastructure Performance:
- Infrastructure Scalability: Expanding the infrastructure in number of processors, networks or storage should have incrementally better impacts on application reliability and performance.
- Record Immutability: For transaction ledgers, all confirmed records and changes are final. This is required by the blockchain protocol.
Note that in practice, record immutability is much harder to achieve than expected. There are two challenges, a) 51% attacks can literally wipe out all histories if successful, and b) for protocols require all nodes to hold independently verified ledger, such as the Bitcoin, the storage requirement grows approximately 50GB per month. It is conceivable that the chain would collapse when all nodes' storage capacity is saturated. Dividing the chain into fixed "shards" can mitigate the eventuality for a while but cannot avoid the ultimate demise.
Protocol Design and Proofs
Before building a robust protocol for infrastructure computing, there are well-known impossibilities and possibilities in physics and computer science that must be thoroughly examined and considered.
The first challenge is infrastructure reliability. A computing infrastructure must deploy multiple components including computing, networking and storage. An infrastructure protocol defines how applications can compute, communicate and store results. A formal proof was found that it is impossible for reliable communication in the face of arbitrary crashes [17]. The laws of physics regarding component reliability [18] show that 100% component reliability is not possible. These facts require that the infrastructure protocol (program-program communication protocol) provide complete component (processing, networking and storage) decoupling from application program logics. This decoupling requirement forces the protocol to exploit "decentralized" or "stateless" components that the legacy infrastructure protocols, such as message passing interface (MPI), remote procedure call (RPC) and remote method invocation (RMI), cannot handle. The blockchain protocol is an example of a "best effort" availability protocol.
Quantifying infrastructure reliability can be traced back to the computer pioneer von Neumann. In addition to his contribution to computer architecture, von Neumann also penned a study on building reliable systems using unreliable components using probabilistic logics, in early fifties [19]. The Internet was built using statistic multiplexed communication protocols. Probabilistic logic is the only possible definition for infrastructure reliability. In literature, this is referred to as "best effort" reliability. Ironically, this best effort reliability also enabled the Internet's infinite scalability -- the benefit we enjoy now and into the future.
The Bitcoin protocol exploits multiple anonymous decoupled (or decentralized) computers connected through the Internet protocol. Judging from the Bitcoin network's reliability to date [20], von Neumann's theory seems working well.
The second challenge involves infrastructure performance. Since the infrastructure must deploy multiple computing, networking and storage components, unless all components can be fully exploited at any scale, incremental performance delivery is impossible. Thus, von Neumann's statistic multiplexing theory must also apply here. The result is a new computing paradigm: Statistic Multiplexed Computing (SMC). The existing blockchain protocols lack this capability.
The infrastructure scalability challenge is automatically resolved once the performance challenge is resolved without negatively impacting reliability -- "best effort" performance" meets "best effort reliability". This requires inductive performance and reliability measures or deliveries.
However, monotonically increasing performance may reach some theoretical limits. Thus, the only remaining challenge is Finality -- can any blockchain protocol design practically deliver true ledger finality in perpetuity?
Theoretically, an inductive statistic multiplexed blockchain protocol is needed to meet the scalability challenge. Non-inductive solutions such as fixed chain "sharding" or "Danksharding" [21] will only increase protocol development complexity with persistent performance walls.
A Scalability Solution
An effective scalability solution can have two practical assumptions:
- The computation problem size can expand indefinitely, since every useful infrastructure is expected to solve bigger problems.
- Computing and network resources will continue to grow indefinitely, into the future.
A formal proof requires a parallel computing model, when taking the number of components to infinity, can yield the maximal performance limit under the assumptions. There are two such models: Amdahl's Law [22] and Gustafson's Law [23].
The Amdahl's Law assumes (0<= s <=1), a percentage of serial instructions that cannot be parallelized. Then the (1-s) percentage of instructions can be accelerated using p processors. The Speedup can then be expressed as:
Speedup(p) = (1)
Speedup() = (2)
Taking p to infinity in equation (1) yields equation (2). But this "scaling" step has two different operational semantics: a) increasing p for faster acceleration by reducing the value of (1-s)/p solving the same problem. This will result s asymptotically approaching to 1. Thus the speedup is above bounded to 1. Or b) increasing p to increase the parallel instruction percentage (1-s) by solving bigger problems. This will force s asymptotically approach to 0. Then the speedup is unbounded . This scaling ambiguity has caused more than half century of confusion in the community.
Although quantifying s requires defining the problem size, equations (1) and (2) are equally applicable to any programs solving any problem size with any percentage s. The limit of speedup (2) also does not depend on problem size. However, since Amdahl originally used fixed problem sizes to argue for the validity of not building parallel machines with too many processors, assuming fixed problem size using p processors has been the norm in interpreting Amdahl's law in the past. This assumption has led to the dismal speedup predictions.
This Amdahl's Law interpretation seems to suggest parallel performances following the economic law of diminishing of returns, even though the mathematics model implies more potentials.
In 1988, Gustafson and Barsis at the Sandia National Laboratory conducted parallel computing experiments that seem to suggest potential infinite speedup.
Gustafson's Law was based on measured sequential and parallel elapsed times using p (=1024) processors. A new sequential percentage (0<=x'<=1) can be calculated using p processors. (1-x') is the parallel percentage using p processors.
To estimate accomplished speedup, Gustafson's Law states:
(3)
Scaling p to for equation (3) cannot be done mathematically since s' is dependent on the values of p. For practical applications, the scaling action also has two operational semantics: a) Keep the problem size fixed, adding processors to further reduce the total parallel processing time, this will push for bigger s' asymptotically to 1. Thus speedup is also bounded to 1. Or b) expanding the problem size to allow the parallel part expanded solving bigger problems by simply multiplying (1-s') by p (as shown in the chart below). Even though the chart is mathematically incorrect, equation (3) can be translated to find the real serial percentage s under a single processor. Increasing p in equation(3) will force the translated s asymptotically approaching to 0. Speedup will be above bounded to by Amdahl's equation (2).
For some reason, in late 1980's, Gustafson's Law was used to argue for Massively Parallel Computing (MPC) (or ManyCPU) experiments and Amdahl's Law was used to argue for bigger mainframe (or BigCPU) computer architectures. These laws have been used to support two diverging computing system experiments and constructions until recent convergence.
It should now be obvious that the two law are identical with Amdahl's Law more succinct. But Gustafson's formula helps to quantify the serial percentages from practical program instrumentation. In fact, the two serial percentages can be related by a simple equation[24]:
(4)
Both laws actually refer to the same mathematical abstraction. Gustafson's formula assists in quantifying the percentage of serial computing through parallel instrumentation. Amdahl's Law then delivers the ultimate predictions. This should have cleared the half-century myth about scaled-speedup and unscaled-speedup.
In practice, extracting parallelism from an algorithm to use more processors is much harder than simply expanding the already parallelized parts to solve bigger problems. This explanation can be validated in practice when developers routinely increasing the problem size to use more parallel processors.
If we plot the full speedup curves against the number of processors, we will see the missing lines from the previous Amdahl's dismal prediction chart.
The TOP500 supercomputer competition provides another proof by a historical log of unrelenting computation power growths where the benchmark (Linpack) having no problem size limit. All manufacturers compete for the world's fastest supercomputer race [25] solving the largest possible Linpack problem that can be handled by the hardware. The follow chart illustrates the continuous speed improvements by year.
In practical blockchain applications, the number of transactions to be processed will increase without a bound. The ledger storage will continue to grow. In practice, the available computing, networking and storage components will continue to grow without bound enabled by the networking protocols. Therefore it is possible to build an infinitely scalable blockchain with these assumption. In particular, a statistic multiplexed computing blockchain can meet any future application needs given proper economic incentives. The infrastructure no longer has the structural deficiency.
Action Plan
These discussions can conclude that in theory, a statistic multiplexed blockchain protocol can deliver infinitely scalable infrastructure in performance and reliability. Leveraging blockchain's data and processing authenticity guarantee via the lock-step cryptographic proofs, infrastructure security is also feasible.
For Toichain protocol design, we choose Bitcoin 24.0.1 as the base line protocol by replacing the PoW consensus by PoS consensus and injecting SMC components into the protocol processing signaling for parallel computing.
This surprising result is also applicable to ledger storage. Without multiplexing, the blockchain ledger storage will eventually saturate all nodes causing the chain to collapse. The SMC blockchain protocol promises to hold the true finality of all transactions in perpetuity by multiplexing all storage resources while keeping the replication factor to a constant.
These discussions follow the inductive logic of the Law of Large Numbers [26].
There are more details for the protocol implementation, especially for Open Source public chains. The protocol implementation must be code tamper resistant, natural disaster and human accident resistant. A secure and performant decentralized consensus protocol is needed.
SMC Proof of Stake Protocol
Existing PoS protocol designs revolved around staking policies and randomness of the selection algorithm. Considering infrastructure scalability will add much complexity to the design. The examples include chain sharding and Danksharding [27].
The challenge is complex -- we must deliver very high performance without compromising security and reliability of the network.
Technically, transaction replication and parallel processing were considered dangerous [28] due to the potential race conditions (or double-spend problem). The blockchain protocol resolved the double-spending problem. It did not solve the parallel processing performance problem.
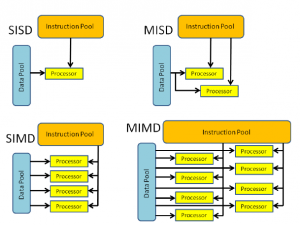
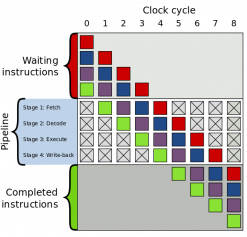
According to Professor Michael Flynn, there are three high-level parallel processing topologies: SIMD (single instruction multiple data), MIMD (multiple instructions multiple data), and pipeline (MISD - multiple instructions single data stream) [29]. However, for eliminating double-spending, all transactions must be serialized, since each block may contain transactions affecting transactions in multiple other blocks. "Race conditions" and non-deterministic results are not allowed. Then the only possible topology entry is pipeline. This means for POS protocol, we must build a pipeline of transaction blocks to be validated without compromising network security and reliability.
The problem is that the nature of the blockchain protocol is that all nodes run independently in parallel with little communication with other nodes via "gossip" protocols. It is far easier to force all nodes store the entire ledger than forcing them to form any pipeline and store partial chain data.
ACAN (Active Content Addressable Network) [U.S. PTO #11,588,926 B2, EPO #3539261]
ACAN is a high-level data communication and synchronization protocol with a SMC (statistic multiplexed computing) runtime that completely decouples all hardware components from communicating programs for network-scale high performance computing. The need for complete component decoupling was implemented in the original blockchain protocol via "gossip" protocol. This delivered blockchain's high availability and security. The simple "gossip" implementation in existing protocols is insufficient for parallel processing signaling.
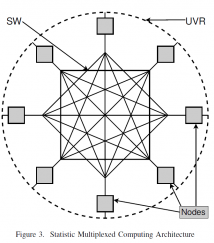
The following figure illustrates the concept of ACAN (active content addressable networking) using UVR (unidirectional virtual ring) architecture. The illustrated implementation uses the Tuple Space resource tagging method and gossip protocol for UVR implementation.
ACAN supports three simple APIs:
- read(&key, &value): key holds a search pattern in a "tuple space" where all nodes are connected. value holds the matched tuple, if any. This is a blocking call that a requesting program will be blocked until a pattern-matched tuple is found. The matching tuple remains in the "tuple space".
- get(&key, &value): Same as the "read()" API, except that the matching tuple is removed from the "tuple space".
- put(key, value): Inserts <key, value> into the "tuple space".
The use of "gossip" protocol can accelerate ACAN network saturation time. Applications running on ACAN will automatically form parallel processing topologies: pipeline, SIMD and MIMD without violating the serialization needs of transaction block validation. Replication factor can also be dynamically controlled to spread replicated blocks in randomly chosen hosts.
The highly parallel nature of the blockchain protocol will automatically implement the SMC principle in real time.
The critical feature of this dynamic SMC pipelined architecture is the inductive scaling feature.
The speed up of a pipeline can be represented as: , where p = number of processors in the pipeline, b = total blocks to be processed. Take the number of blocks to infinity:
This means that as long as there are enough blocks to be processed, the entire chain's performance will be above bounded to the number of nodes in the pipeline.
For illustration purposes, the variation of block processing times was not considered in the above calculations. To see the power of pipeline parallelism, the automobile manufacturing processes illustrate a similar situation. The Hyundai Motor Company's production pipelines can produce 3,835 vehicles per day and 1.4M per year[30].
Toichain Tokens
Toichain token is TOIN. There are 50,000,000,000 TOINs for the Alpha Release. There are air-drop tokens for early adopters, 1,000 TOIN each. Users need to register to download a toichain wallet to receive the payment. Citizenship is checked and verified to ensure that US citizens do not apply. The minimal staking contract is 10 TOINs.
Non-Fungible Tokens
The TestNet Release of toichain protocol will support embedding arbitrary data in an "OP_RETURN" transaction that will be permanently recorded on the chain. Unlike the ordinal NFT [31] or NFT (non-fungible token) on other chains, these transactions cannot be altered or removed.
There are practical applications for these forever NFTs. Once Taproot is enabled on toichain, ordinal NFTs (BRC-20) will also be supported. Unlike the original Bitcoin network where BRC-20 craze has created massive network congestion[32], all transactions will be processed promptly in toichain without congestion or scaling problems.
Toichain TestNet Launch
The toichain testnet launch will enable users to interact with one another through simple payments, just like the original Bitcoin network. Forever NFTs are supported. Smart contracts will be supported on a later date.
References
- ↑ https://bitcoin.org/bitcoin.pdf
- ↑ https://www.napster.com/us
- ↑ https://www.bittorrent.com/
- ↑ https://en.wikipedia.org/wiki/Proof_of_work
- ↑ https://www.investopedia.com/terms/p/proof-stake-pos.asp
- ↑ https://identityserver4.readthedocs.io/en/latest/topics/pop.html
- ↑ https://www.infoworld.com/article/3666736/solana-blockchain-and-the-proof-of-history.html
- ↑ https://www.forbes.com/advisor/investing/cryptocurrency/bitcoins-energy-usage-explained/
- ↑ https://messari.io/report/solana-analyzing-downtimes-statistics-and-ecosystem-development
- ↑ https://originstamp.com/blog/has-there-ever-been-a-51-attack-on-bitcoin/#notable-51-attacks
- ↑ https://www.theguardian.com/technology/2014/mar/18/history-of-bitcoin-hacks-alternative-currency
- ↑ https://increditools.com/blockchains/
- ↑ https://sensoriumxr.com/articles/what-is-the-blockchain-trilemma
- ↑ https://medium.com/coinmonks/blockchain-scaling-30c9e1b7db1b
- ↑ https://en.wikipedia.org/wiki/Vitalik_Buterin
- ↑ https://static.ias.edu/pitp/archive/2012files/Probabilistic_Logics.pdf
- ↑ https://groups.csail.mit.edu/tds/papers/Lynch/jacm93.pdf
- ↑ Encyclopedia of Physical Science and Technology, Editor-in-Chief Robert A. Meyers, ISBN 978-0-12-227410-7, 2001
- ↑ https://static.ias.edu/pitp/archive/2012files/Probabilistic_Logics.pdf
- ↑ https://buybitcoinworldwide.com/bitcoin-downtime/
- ↑ https://ethereum.org/en/roadmap/danksharding/
- ↑ https://en.wikipedia.org/wiki/Amdahl%27s_law
- ↑ https://en.wikipedia.org/wiki/Gustafson%27s_law
- ↑ https://www.researchgate.net/publication/228367369_Reevaluating_Amdahl's_law_and_Gustafson's_law
- ↑ https://www.top500.org/
- ↑ https://www.sciencedirect.com/topics/mathematics/laws-of-large-number
- ↑ https://ethereum.org/en/roadmap/danksharding/
- ↑ https://pages.cs.wisc.edu/~yxy/cs764-f20/papers/replication.pdf
- ↑ https://link.springer.com/referenceworkentry/10.1007/978-0-387-09766-4_2
- ↑ https://en.wikipedia.org/wiki/List_of_Hyundai_Motor_Company_manufacturing_facilities
- ↑ https://blog.chain.link/ordinals-bitcoin-nfts/
- ↑ https://beincrypto.com/learn/brc-20-token/
Consult the User's Guide for information on using the wiki software.