Main Page

Welcome to Twiki -- A Toichain Wiki

This is the unofficial Toichain wiki site. Content on this site is subject to frequent changes.

---

Introduction

The blockchain protocol was introduced via a paper entitled "Bitcoin: A peer-to-peer Electronic Cash System" by Satoshi Nakamoto in 2008. Although there were other peer-to-peer file-sharing projects before this time, such as Napster and Bittorrent , and other electronic currency attempts, the Bitcoin project demonstrated the strongest staying power compared even to the currently running 23,000+ other blockchains. Unlike the new cryptocurrencies, the Bitcoin is often referred to as "digital gold" for its scarcity, there are only 21 million hard-coded Bitcoins in the protocol. Other protocols (and associated cryptos) have different token supply amount and distribution policies.

The most attractive common blockchain features are the decentralized consensus-driven decision making process and step-by-step cryptographic proving system. In addition to cryptocurrencies, there are many applications that can benefit from such a secure store of value with reliable transaction ledger without any third-party involvements.

Before trying to understand the Blockchain protocol and its variants, it is important to understand the differences between an algorithm and a protocol.

In general, an algorithm is a program that runs on a single computer solving a single problem. A protocol, however, is a program that runs on all computers in parallel solving a single problem. An algorithm must be transformed to run on all computers in parallel solving the same problem before it to be called a protocol. Therefore, protocol development is significantly more difficult than algorithms.

Consensus Protocols

A good consensus protocol in a blockchain system has at least four properties:

1. Fault tolerance to defend failures caused by natural disasters and human hacks or accidents
2. Byzantine failure tolerance to defend exploitation by colluding parties
3. Centralization avoidance to prevent corruptions in the decision making process
4. Source code tamper resistance to automatically reject malicious attacks

Without assuming all nodes active at all times, the blockchain rely on "gossip" protocol to communicate with other nodes. There are two popular types of consensus protocols: Proof of Work (POW) or Proof of Stake (POS) . Others include Proof of Possession(POP), Proof of History(POH). The ultimate goal is to eliminate double-spending, even if some nodes maybe tampered to attack the integrity of the network, since the protocols are Open Source.

The Bitcoin network uses POW that forces participating miners to compete for the fastest hashing rate by solving a compute intensive cryptographic puzzle. Although it withstood more than 14 year of battle ground tests, it has suffered criticism on escalating electricity consumption . The POH network Solana suffered multiple single-point-failure incidents . All protocols are susceptible to 51% attacks .

Since 2009, Bitcoin has been proven the strongest against the common hacks . As the POW puzzle difficulty has increased dramatically over the years, the probability of 51% attack on the Bitcoin network becomes more difficult. POS protocols can save more than 90% energy consumption compared to POW chains. According to Forbes, there are 80 cryptocurrencies use POS protocols at the time of this writing.

There are approximately 1,000 blockchains in four types: public, private, consortium, and permissioned .

Cryptographic Proofs

The Blockchain protocol relies on UTXO (unspent transaction output) model and lock-step cryptographic proofs to authenticate every transaction. Once spent, the UTXO is destroyed. Double-spending is theoretically impossible. Each proof step must be executed on a script engine running the same protocol on all nodes. The concurrently produced results are confirmed by the consensus protocol mentioned above and committed to the chain.

Blockchain Trilemma

Blockchain protocols have three common aspects: security, decentralization and scalability -- the three terms that do not have precise definitions but intuitively understood . To date, the existing cryptographic tools have been proven effective for transaction security before the introduction of smart contracts. Decentralization is given by the nature of the protocols. In theory, there should be no service downtimes unless the entire network is down and all nodes crash at the same time. The scalability challenge eludes to deliverable performance and transaction finality which remained unclear.

The trilemma was first introduced by Vitalik Buterin, one of the co-founders of Ethereum network. The problems are real. There seems no obvious solutions to accomplish all three goals using known methods. Therefore, all proposed solutions revolve around reducing "opportunity costs" focusing only on partial goals.

Treating the blockchain network as an infrastructure for transaction processing, one would find the trilemma was only an extension of the legacy infrastructure scaling performance and reliability dilemma, where "infrastructure reliability" also does not have a commonly accepted definition. Fortunately all these metrics, although important, are non-functional. Every proposed solution can be a feasible solution with varying "opportunity costs". There was also no obvious solutions to overcome the dilemma.

Statistic Multiplexed Computing (SMC)

The principle of using unreliable components to build arbitrarily reliable system was first lectured by von Neumann in early fifties. The idea was to use probabilistic logic to quantify the reliability of a system by multiplexing all components. This theory was applied to the construction of Internet protocols to deliver the "best effort" performance and reliability. Incidentally, the best effort reliability and performance enabled the unlimited scalability of the Internet. It is possible to apply the same methodology to distributed and decentralized computing.

Definitions

It helps to define the challenging metrics more precisely as infrastructure protocol design guidelines. For definitions #1 and #2, the word "infrastructure" implies all applications running on the infrastructure.

1. Infrastructure Reliability: MTBF (mean time between failure) = ${\frac {\sum ((Start-Of-Downtime)-(Start-of-uptime))}{No-of-failures}}$
2. Infrastructure Performance: ${\frac {No-of-Transactions}{Second}}$
3. Infrastructure Scalability: Expanding the infrastructure in number of processors, networks or storage should have incrementally better impacts on reliability and performance.
4. Record Immutability: For transaction ledgers, all records and changes are final. This is required for blockchain ledger infrastructures.

Protocol Design and Proofs

Before building a robust protocol for infrastructure computing, there are well-known impossibilities and possibilities in physics and computer science that must be thoroughly examined for extreme cases.

The first challenge is infrastructure reliability. A computing infrastructure must deploy multiple components including computing, networking and storage. An infrastructure protocol defines how applications can compute, communicate and store results. A formal proof was found that it is impossible for reliable communication in the face of arbitrary crashes . The laws of physics dictate component reliability that 100% component reliability is not possible. These facts demands the infrastructure protocol (program-program communication protocol) to provide complete component (processing, networking and storage) decoupling from application program logics. This decoupling requirement forces the protocol to exploit "decentralized" or "stateless" components that the legacy infrastructure protocols, such as message passing interface (MPI), remote procedure call (RPC) and remote method invocation (RMI), cannot handle. The blockchain protocol is such an example of high availability protocol.

Quantifying infrastructure reliability can be traced back to the computer pioneer von Neumann. In addition to his contribution to computer architecture, von Neumann also penned a study on building reliable system using unreliable components using probabilistic logics in early fifties . The Internet was built using statistic multiplexed communication protocols. Probabilistic logic is the only possible definition for infrastructure reliability. In literature, this is referred to as the "best effort" reliability. Ironically, this best effort reliability also enabled the Internet's infinite scalability -- the benefit we enjoy now and into the future.

The Bitcoin protocol exploits multiple anonymous decoupled (or decentralized) computers connected through the Internet protocol. Judging from the Bitcoin network's reliability to date , von Neumann's theory seems working well.

The second challenge is infrastructure performance. Since the infrastructure must deploy multiple computing, networking and storage components, unless all components can be fully exploited in any scale, incremental performance delivery is impossible. Thus, von Neumann's statistic multiplexing theory must also apply here. The result is a new computing paradigm: Statistic Multiplexed Computing (SMC). The existing blockchain protocols fall short.

Infrastructure scalability challenge is automatically resolved once the performance challenge is resolved without negatively impacting reliability -- "best effort" performance" meets "best effort reliability".

However, monotonically increasing performance may reach some theoretical limits. Thus, the only remaining challenge is Finality -- can any blockchain protocol design practically deliver true ledger finality in perpetuity?

Theoretically, only statistic multiplexed blockchain protocol can meet the scalability challenge.

Scalability Proof

The proof makes two assumptions:

• The computation problem size can expand indefinitely, since every useful infrastructure is expected to solve bigger problems.

• There are infinite supplies of computing, networking and storage components in time.

Amdahl's Law Speedup Predictions

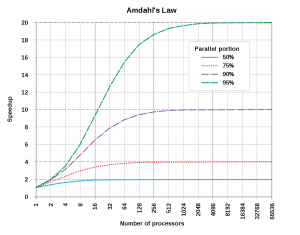
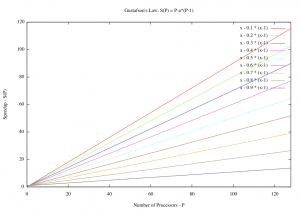
A formal proof requires a parallel computing model, when taking the number of components to infinity, can yield the maximal performance limit under the assumptions. There are two such models: Amdahl's Law and Gustafson's Law . The problem is that these two "laws" seem to yield complete opposite performance predictions.

The Amdahl's Law seems to predict parallel performances following the economic law of diminishing of returns while Gustafson's Law seems to lead infinite speedups. Gustafson's Law was used to argue for Massively Parallel Computing (MPC) experiments and Amdahl's Law was used to argue for bigger supercomputer constructions. In the last three decades, these laws have been used to build parallel computing systems and multi-processor operating systems and computing clouds.

Gustafson's Law

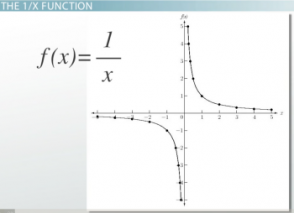
A careful examination revealed that the two laws are mathematically dependent where Amdahl's formulation has a tight peak performance bound $\left({\frac {1}{x}}\right)$ when taking the number of parallel processors to infinity, where x = the percentage of serial portion of instructions in a program. This means that the peak performance of every parallel program is above-bounded to $\left({\frac {1}{x}}\right)$, when $\chi \Longrightarrow 0$, the performance will asymptotically approach to $\infty$, when $\chi \Longrightarrow 1$ the speedup will approach 1. Thus, if the computing problem's size is fixed, x will eventually approach to 1 as the number of processors increases -- economic law of diminishing of return. If the problem size is open (solving bigger problems), then increasing the number of processors will force x to approach 0. The challenge is that quantifying $\chi$ for any practical parallel program is very hard. Gustafson's Law was derived from running actual parallel programs. It can be easily used to quantify $\chi$ in Amdahl's Law for any practical parallel program.

This model can be validated in practice when developers simply increasing the problem size to use more parallel processors.

Amdalh's Law and Peak Parallel Performance

A classical example is the TOP500 supercomputer benchmarks (linear solvers) that have open problem sizes for all manufacturers to compete in the world's fastest supercomputer race .

In practical blockchain applications, the number of transactions to be processed will increase until it satisfies all possible requests. The available computing, networking and storage components can easily cover the needs given proper incentives.

Conclusion

These discussions can conclude that in theory, a statistic multiplexed blockchain protocol can deliver infinitely scalable infrastructure in performance and reliability. Leveraging blockchain's data and processing authenticity guarantee via the lock-step cryptographic proofs, infrastructure security is also feasible.

This surprising result is also applicable to ledger storage. Without multiplexing, the blockchain ledger storage will eventually saturate all nodes causing the chain to collapse. The SMC blockchain protocol promises to hold the true finality of all transactions in perpetuity.

These discussions also follow the Law of Large Numbers .

There are more details for the protocol implementation, especially for Open Source public chains. The protocol implementation must be code tamper resistant, natural disaster and human accident resistant. A secure and performant decentralized consensus protocol is needed.

SMC Proof of Stake Protocol

There are many POS protocol designs.

- Statistic Multiplexed Computing - Statistic multiplexing method was first proposed in 1952 by von Neumann.

- Statistic Multiplexed Blockchain -

References

Consult the User's Guide for information on using the wiki software.

Getting started

• Configuration settings list
• MediaWiki FAQ
• MediaWiki release mailing list
• Localise MediaWiki for your language
• Learn how to combat spam on your wiki